Use of the Neural Network Class with two sample applications.
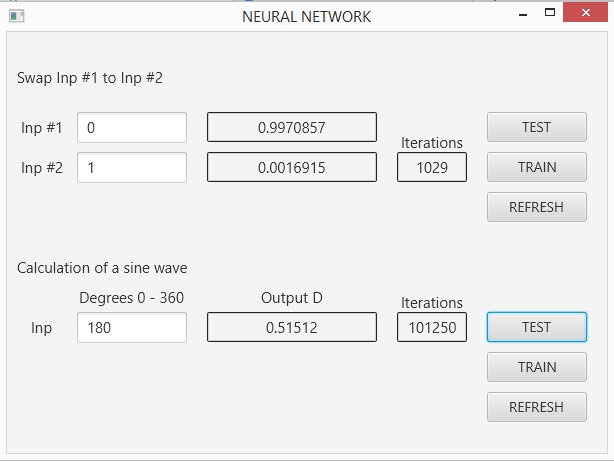
NEURAL NETWORK
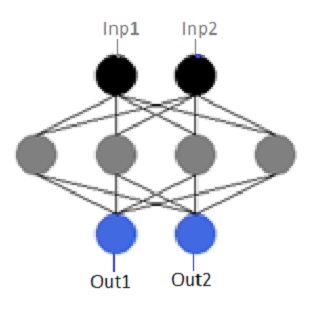
Swap Inp #1 to Inp #2
Learning rate 22.5
To obtain sufficiently exact values, reach 1,000 iterations.
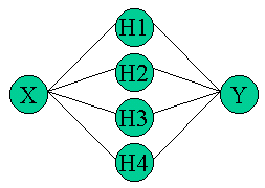
Calculation of a sine wave.
Learning rate 0.5
In input we provide a value between 0 and 1 representing the angle between 0 and 360 degrees, and in output we obtain the sine of the angle in the range 0.1..0.9 (the value from 0.1 to 0.9 at the exit must represent the sine from -1 to +1).
The reason for having an output range of 0.1 to 0.9 is that to get exactly to the limits 0 and 1 we need very large weights, while it is relatively simple to get to 10% or 90%.
The following table shows 17 samples of the value of the sine taken in the whole range 0..360 degrees. The column Input X represents the input of the network, that is the degrees translated in the range 0..1 through the formula:
X = degrees / 360
The output column D instead represents the desired values of sine (X) translated in the range 0.1..0.9 through the formula:
D = 0.1 + (0.8 * (sine + 1) / 2)
To obtain sufficiently exact values, reach 100,000 iterations.
This project is free and Donate too.
Bitcoin: 3D5DVx5rPB14sUNbZbiYotZ1DLypqcBTed
Paypal: https://paypal.me/ClaudioGal
NEURAL NETWORK
Swap Inp #1 to Inp #2
Learning rate 22.5
To obtain sufficiently exact values, reach 1,000 iterations.
Calculation of a sine wave.
Learning rate 0.5
In input we provide a value between 0 and 1 representing the angle between 0 and 360 degrees, and in output we obtain the sine of the angle in the range 0.1..0.9 (the value from 0.1 to 0.9 at the exit must represent the sine from -1 to +1).
The reason for having an output range of 0.1 to 0.9 is that to get exactly to the limits 0 and 1 we need very large weights, while it is relatively simple to get to 10% or 90%.
The following table shows 17 samples of the value of the sine taken in the whole range 0..360 degrees. The column Input X represents the input of the network, that is the degrees translated in the range 0..1 through the formula:
X = degrees / 360
The output column D instead represents the desired values of sine (X) translated in the range 0.1..0.9 through the formula:
D = 0.1 + (0.8 * (sine + 1) / 2)
B4X:
' Samples Degrees Sine Input X Output D
' 1 0.0 0.0000 0.0000 0.5000
' 2 22.5 0.3827 0.0625 0.6531
' 3 45.0 0.7071 0.1250 0.7828
' 4 67.5 0.9239 0.1875 0.8696
' 5 90.0 1.0000 0.2500 0.9000
' 6 112.5 0.9239 0.3125 0.8696
' 7 135.0 0.7071 0.3750 0.7828
' 8 157.5 0.3827 0.4375 0.6531
' 9 180.0 0.0000 0.5000 0.5000
' 10 202.5 -0.3827 0.5625 0.3469
' 11 225.0 -0.7071 0.6250 0.2172
' 12 247.5 -0.9239 0.6875 0.1304
' 13 270.0 -1.0000 0.7500 0.1000
' 14 292.5 -0.9239 0.8125 0.1304
' 15 315.0 -0.7071 0.8750 0.2172
' 16 337.5 -0.3827 0.9375 0.3469
' 17 360.0 0.0000 1.0000 0.5000To obtain sufficiently exact values, reach 100,000 iterations.
This project is free and Donate too.
Bitcoin: 3D5DVx5rPB14sUNbZbiYotZ1DLypqcBTed
Paypal: https://paypal.me/ClaudioGal
