Hi everybody:
I am presenting the idea of protecting a developer library ( or any app) with a password.
I wrote a Latitude-Longitude library to find the distance, bearing, and midpoint, to a very high precision, between two geolocations in terms of their latitudes and longitudes.
Each function of the three is included in a sub as follows:
The library can be updated with any function.
A function called password that takes a string as a parameter will check for functions whether to be implemented or not as follows:
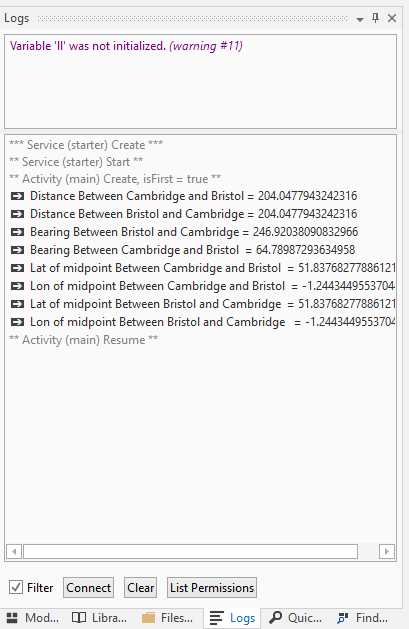
So if the password "xxxxxxxxxxx" is the correct one, the user will be given access to the functions. The algorithm of password generator implies a string with a certain number and sequence of letters.
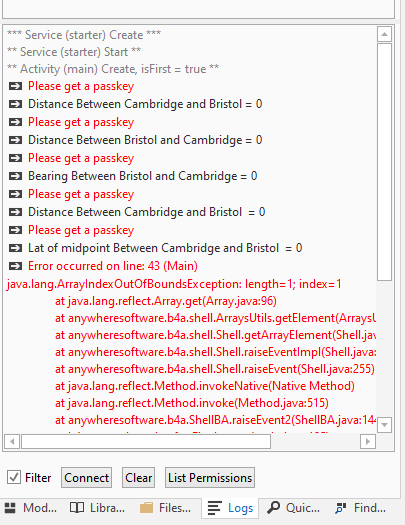
If the password is not correct, no function is carried out and a notice will appear in the log.
Anyone who puts a like and comments will be eligible to receive the library password by DM.
The source code can be purchased at $25 by PayPal
I am presenting the idea of protecting a developer library ( or any app) with a password.
I wrote a Latitude-Longitude library to find the distance, bearing, and midpoint, to a very high precision, between two geolocations in terms of their latitudes and longitudes.
Each function of the three is included in a sub as follows:
- DisBetweenLatLong(Lat1 As Double,Long1 As Double,Lat2 As Double,Long2 As Double) As Double
- BearingBetweenLatLon(Lat1 As Double,Long1 As Double,Lat2 As Double,Long2 As Double) As Double
- MidPointBetweenLatLon(Lat1 As Double,Long1 As Double,Lat2 As Double,Long2 As Double) As Double()
- Util_convert_lat_long(Lat_long_string As String) As Double
The library can be updated with any function.
A function called password that takes a string as a parameter will check for functions whether to be implemented or not as follows:
B4X:
Sub Process_Globals
'These global variables will be declared once when the application starts.
'These variables can be accessed from all modules.
Private ll As Latlong
End Sub
'
'
'
Sub Activity_Create(FirstTime As Boolean)
Activity.LoadLayout("Layout")
ll.password("xxxxxxxxxx")
Log("Distance Between Cambridge and Bristol = " & ll.DisBetweenLatLong(52.2053,0.1218,51.4545,-2.5879))
Log("Distance Between Bristol and Cambridge = " & ll.DisBetweenLatLong(51.4545,-2.5879,52.2053,0.1218))
Log("Bearing Between Bristol and Cambridge = " & ll.BearingBetweenLatLon(52.2053,0.1218,51.4545,-2.5879))
Log("Distance Between Cambridge and Bristol = " &ll.BearingBetweenLatLon(51.4545,-2.5879,52.2053,0.1218))
Dim coor(2) As Double
coor= ll.MidPointBetweenLatLon(52.2053,0.1218,51.4545,-2.5879)
Log("Lat of midpoint Between Cambridge and Bristol = " & coor(0) )
Log("Lon of midpoint Between Cambridge and Bristol = " & coor(1) )
coor=ll.MidpointBetweenLatLon(51.4545,-2.5879,52.2053,0.1218)
Log("Lat of midpoint Between Bristol and Cambridge = " & coor(0) )
Log("Lon of midpoint Between Bristol and Cambridge = " & coor(1) )
End SubSo if the password "xxxxxxxxxxx" is the correct one, the user will be given access to the functions. The algorithm of password generator implies a string with a certain number and sequence of letters.
If the password is not correct, no function is carried out and a notice will appear in the log.
Anyone who puts a like and comments will be eligible to receive the library password by DM.
The source code can be purchased at $25 by PayPal
Attachments
Last edited:
