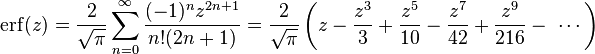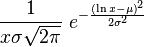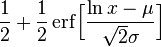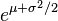Hi
After viewing Erel's video I managed to produce a simple library.
I used the C# code of the B4PPC Probability library and very easily converted it to Java.
The library caculates the Probability density and commulative functions of:
Normal, ChiSquare, Student, Fisher F, Rayleigh, Erlang, Binomial, Geometric, Poisson and Exponential.
It also includes Random Number Generators with some of the distributions (as B4a has only uniform distribution random numbers), and some mathematical functions that are related to distributions: Beta, Gamma, Factorial and Double Factorial, NChooseK
Please check and let me know if it is understandable.
Edit: updated to correct documentation.
Edit: This version of documentation must be better...
Edit: attached an example program.
After viewing Erel's video I managed to produce a simple library.
I used the C# code of the B4PPC Probability library and very easily converted it to Java.
The library caculates the Probability density and commulative functions of:
Normal, ChiSquare, Student, Fisher F, Rayleigh, Erlang, Binomial, Geometric, Poisson and Exponential.
It also includes Random Number Generators with some of the distributions (as B4a has only uniform distribution random numbers), and some mathematical functions that are related to distributions: Beta, Gamma, Factorial and Double Factorial, NChooseK
Please check and let me know if it is understandable.
Edit: updated to correct documentation.
Edit: This version of documentation must be better...
Edit: attached an example program.
Attachments
Last edited: