Hi
I developed a power supply monitoring system which processes and displays large amounts of data and provides statistics as well as graphical displays. I cannot post this project because it relies on large databases for its operation.
I extracted some of the code I developed and put it in a simple demo app as other people might find the code useful.
FILTERING
The app demonstrates the use of single order lag filters for graphical data smoothing.
The are of two types:
- Single order forward filters
- Single order zero phase filters
Most people use moving averages to filter their data for visualization, however these suffer from a number of issues:
- Heavy filtering requires a large number of filter bins each of which requires a summation
- The filter introduces a time delay proportional to half the period of the span covered by the bin samples
- Special consideration must be given to the ends of the data, such as padding with constants to provide room for the bins. i.e the first sample has only itself and it is only on the sample equal to the number of bins that a full average may be carried out
A simpler filter is the single order difference equation where:
y(0) = x(0)
y(n) = y(n-1) + Ts / (Ts + tc) * ( x(i) - y(i-1) )
Where:
x = input sequence
y = output sequence
Ts = Sample time in seconds
Tc = Filter time constant in seconds.
To calculate the cutoff frequency of the filter:
f = 1 / (2* Pi * tc)
The single order difference equation simulates a single order real transfer function, i.e simple RC filter.
Of course the filter "delays" the signal in the same way that a moving average does. However by implementing two identical filters, time reversing the signals twice the phase error may be completely cancelled:
The process is:
x(t) => lagFilter => y1(t) => reverse y1(t) => yr(t) => lagFilter => reverse yr(t) = y(t)
Mathematically it may be shown that the filter has no effect on the phase of the signals. The maths for this is provided in:
Stack Exchange - Zero Phase Filter
Its quite simple to understand. However without resorting to maths if we filter a signal in the forward then back direction for any given input frequency the phase error incurred in the first pass is negative, whilst in the second reversed pass the phase error is positive so they simply cancel. So it can also be explained in plain English.
This same technique can be used for moving averages which are special case of Finite Impulse Response (FIR) filters and also for Infinite Impulse response (IIR) Filters of which the first order lag is a special case as it only includes real, not complex poles in its design. However the algorithms become complicated and slower because of the need to deal with the multiple filter states. In the case of the single order lag only the output state is required.
Of course the filter cannot be used real-time as you cannot reproduce the sequence in reverse, however for static data visualization you can see from the example that the zero phase filtered signal lines up with the input whereas the non-zp filter delays the signal.
The zp filter is non causal in that the output precedes the input, however the shape of the pulse is much better maintained albeit with slopes on the leading and trailing edges.
When you start the app you will see:
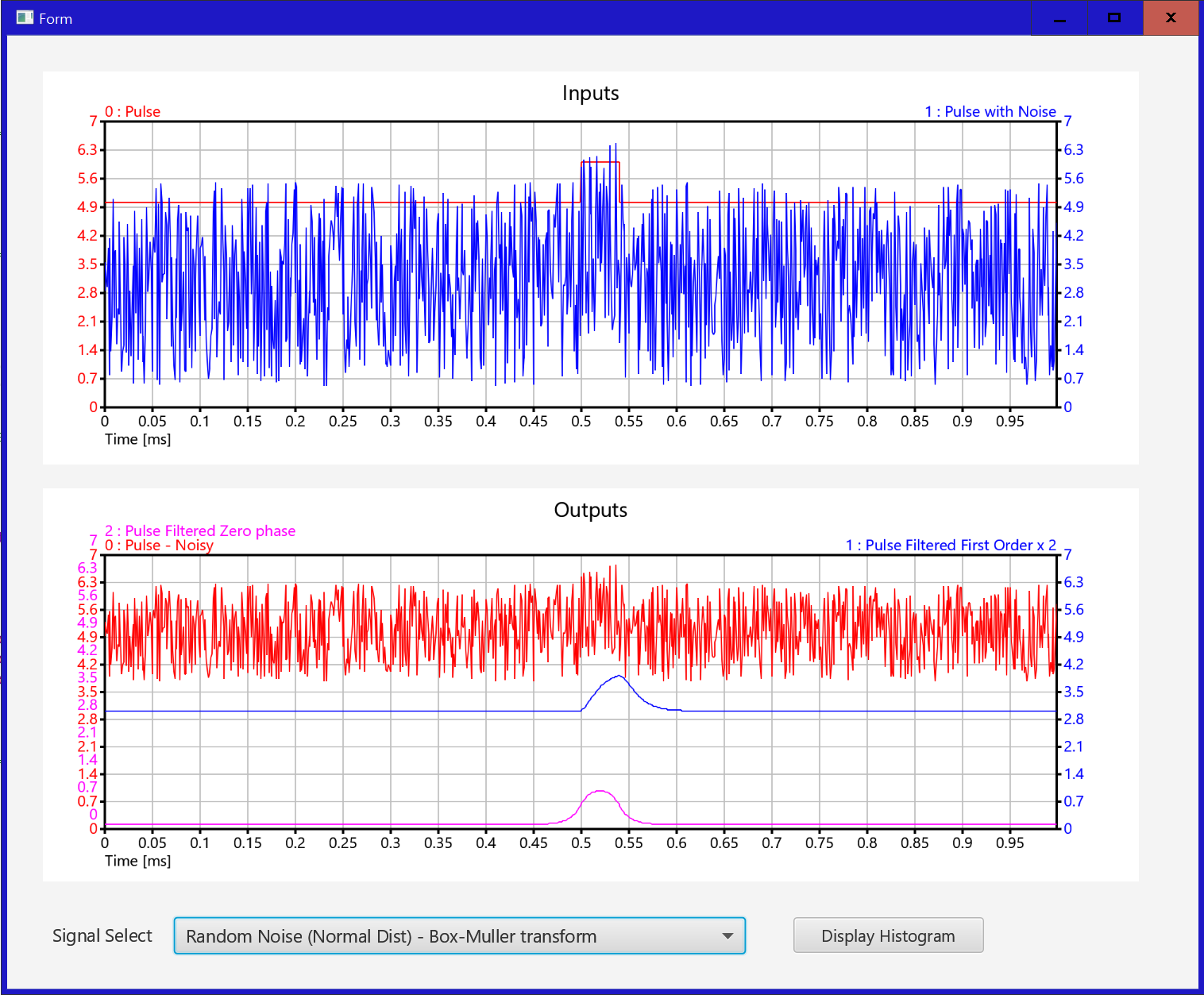
The top graph shows the input and the input with uniform distributed random noise added.
The bottom one shows the noisy signal (red) and the filtered signals.
The Blue is filtered twice by a single order lag
The Magenta is the same noisy signal filtered by the zero phase filter.
The code for the filters isn't optimized as I didn't want to obscure the functionality in clever coding and the filters can process thousands of samples very quickly so there didn't seem to be a lot of point.
HISTOGRAM
The second feature of the app is the histogram. This is implemented as a custom view and uses, xChart to display the histograms.
It's not a highly polished product as it wasn't developed for general use. Some of the code is left over from my Power Monitor App.
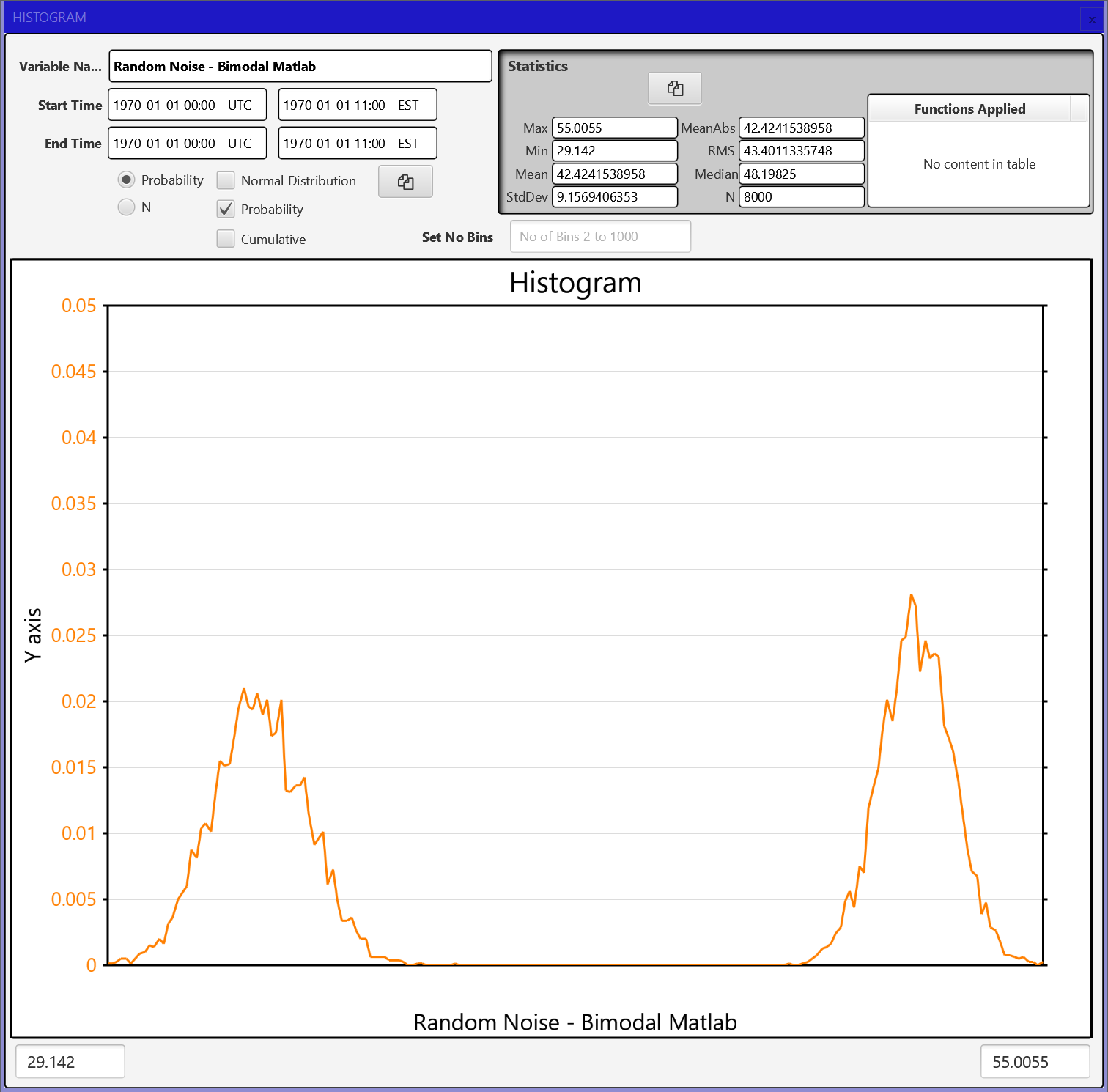
To get the histogram function to operate select a signal in the drop-down and push the Display Histogram button. The signal is displayed in the bottom graph and a modal dialog opens with the histogram plot and various calculated stats.
I tried using the rand function and the Box-Muller transform to create normal distributions, however they are pretty crummy. I don't know whether this is because the b4x random function isn't that random or whether I haven't implemented the Box-Muller transform properly. So I used Matlab to generate an 8000 point signal with a normal distribution and included that as a test signal as well.
Hope this stuff may be of use
Best regards
Rob
I developed a power supply monitoring system which processes and displays large amounts of data and provides statistics as well as graphical displays. I cannot post this project because it relies on large databases for its operation.
I extracted some of the code I developed and put it in a simple demo app as other people might find the code useful.
FILTERING
The app demonstrates the use of single order lag filters for graphical data smoothing.
The are of two types:
- Single order forward filters
- Single order zero phase filters
Most people use moving averages to filter their data for visualization, however these suffer from a number of issues:
- Heavy filtering requires a large number of filter bins each of which requires a summation
- The filter introduces a time delay proportional to half the period of the span covered by the bin samples
- Special consideration must be given to the ends of the data, such as padding with constants to provide room for the bins. i.e the first sample has only itself and it is only on the sample equal to the number of bins that a full average may be carried out
A simpler filter is the single order difference equation where:
y(0) = x(0)
y(n) = y(n-1) + Ts / (Ts + tc) * ( x(i) - y(i-1) )
Where:
x = input sequence
y = output sequence
Ts = Sample time in seconds
Tc = Filter time constant in seconds.
To calculate the cutoff frequency of the filter:
f = 1 / (2* Pi * tc)
The single order difference equation simulates a single order real transfer function, i.e simple RC filter.
Of course the filter "delays" the signal in the same way that a moving average does. However by implementing two identical filters, time reversing the signals twice the phase error may be completely cancelled:
The process is:
x(t) => lagFilter => y1(t) => reverse y1(t) => yr(t) => lagFilter => reverse yr(t) = y(t)
Mathematically it may be shown that the filter has no effect on the phase of the signals. The maths for this is provided in:
Stack Exchange - Zero Phase Filter
Its quite simple to understand. However without resorting to maths if we filter a signal in the forward then back direction for any given input frequency the phase error incurred in the first pass is negative, whilst in the second reversed pass the phase error is positive so they simply cancel. So it can also be explained in plain English.
This same technique can be used for moving averages which are special case of Finite Impulse Response (FIR) filters and also for Infinite Impulse response (IIR) Filters of which the first order lag is a special case as it only includes real, not complex poles in its design. However the algorithms become complicated and slower because of the need to deal with the multiple filter states. In the case of the single order lag only the output state is required.
Of course the filter cannot be used real-time as you cannot reproduce the sequence in reverse, however for static data visualization you can see from the example that the zero phase filtered signal lines up with the input whereas the non-zp filter delays the signal.
The zp filter is non causal in that the output precedes the input, however the shape of the pulse is much better maintained albeit with slopes on the leading and trailing edges.
When you start the app you will see:
The top graph shows the input and the input with uniform distributed random noise added.
The bottom one shows the noisy signal (red) and the filtered signals.
The Blue is filtered twice by a single order lag
The Magenta is the same noisy signal filtered by the zero phase filter.
The code for the filters isn't optimized as I didn't want to obscure the functionality in clever coding and the filters can process thousands of samples very quickly so there didn't seem to be a lot of point.
HISTOGRAM
The second feature of the app is the histogram. This is implemented as a custom view and uses, xChart to display the histograms.
It's not a highly polished product as it wasn't developed for general use. Some of the code is left over from my Power Monitor App.
To get the histogram function to operate select a signal in the drop-down and push the Display Histogram button. The signal is displayed in the bottom graph and a modal dialog opens with the histogram plot and various calculated stats.
I tried using the rand function and the Box-Muller transform to create normal distributions, however they are pretty crummy. I don't know whether this is because the b4x random function isn't that random or whether I haven't implemented the Box-Muller transform properly. So I used Matlab to generate an 8000 point signal with a normal distribution and included that as a test signal as well.
Hope this stuff may be of use
Best regards
Rob
