The attached project wraps the ZXING part of this Github project. I have not tested all the barcode formats but it should scan the following types:
BarcodeFormat.UPC_A
BarcodeFormat.UPC_E
BarcodeFormat.EAN_13
BarcodeFormat.EAN_8
BarcodeFormat.RSS_14
BarcodeFormat.CODE_39
BarcodeFormat.CODE_93
BarcodeFormat.CODE_128
BarcodeFormat.ITF
BarcodeFormat.CODABAR
BarcodeFormat.QR_CODE
BarcodeFormat.DATA_MATRIX
BarcodeFormat.PDF_417
Please take note of the xml files in the /Objects/res/layout and Objects/res/values folders of the B4A project should you start a new project from scratch.
Posting the following:
1. B4A project demonstrating the Barcode Scanner
2. B4A library files - copy them to your additional library folder
3. You also need android-support.v4.jar and core-3.2.1.jar to be in your additional library folder. I have zipped them together and you can download them from this link:
https://www.dropbox.com/s/h9ts6cjfoo5et6h/core-3.2.1.zip?dl=0
You can use it in portrait mode and landscape mode by changing the B4A project's attribute and the code in the Designer:
#SupportedOrientations: portrait
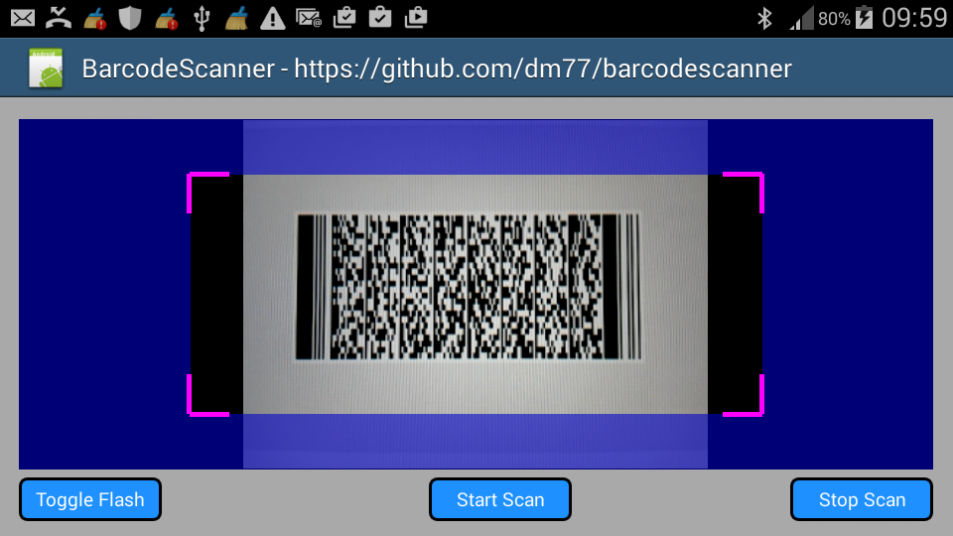
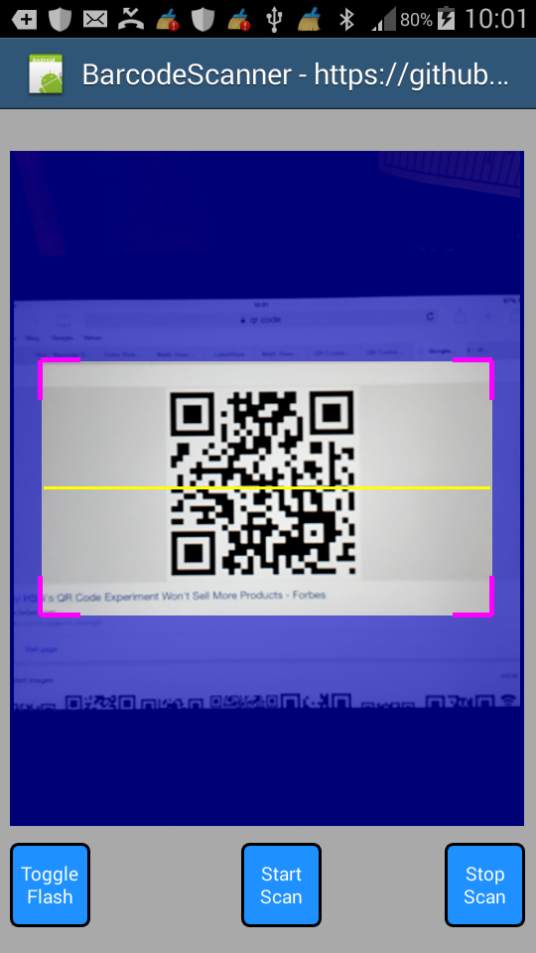
Sample code:
The library:
ZxingBarcodeScanner
Author: Github: Dushyanth Maguluru, Wrapped by: Johan Schoeman
Version: 1
ZxingBarcodeScanner
Events:
BarcodeFormat.UPC_A
BarcodeFormat.UPC_E
BarcodeFormat.EAN_13
BarcodeFormat.EAN_8
BarcodeFormat.RSS_14
BarcodeFormat.CODE_39
BarcodeFormat.CODE_93
BarcodeFormat.CODE_128
BarcodeFormat.ITF
BarcodeFormat.CODABAR
BarcodeFormat.QR_CODE
BarcodeFormat.DATA_MATRIX
BarcodeFormat.PDF_417
Please take note of the xml files in the /Objects/res/layout and Objects/res/values folders of the B4A project should you start a new project from scratch.
Posting the following:
1. B4A project demonstrating the Barcode Scanner
2. B4A library files - copy them to your additional library folder
3. You also need android-support.v4.jar and core-3.2.1.jar to be in your additional library folder. I have zipped them together and you can download them from this link:
https://www.dropbox.com/s/h9ts6cjfoo5et6h/core-3.2.1.zip?dl=0
You can use it in portrait mode and landscape mode by changing the B4A project's attribute and the code in the Designer:
#SupportedOrientations: portrait
B4X:
zx1.Left = 2%x
zx1.Top = 5%y
zx1.Width = 96%x
zx1.Height = 80%y
b1.Left = 2%x
b1.Top = zx1.Bottom + 2%y
b1.Width = 15%x
b1.Height = 10%y
b2.Left = 45%x
b2.Top = zx1.Bottom + 2%y
b2.Width = 15%x
b2.Height = 10%y
b3.Left = 83%x
b3.Top = zx1.Bottom + 2%y
b3.Width = 15%x
b3.Height = 10%ySample code:
B4X:
#Region Project Attributes
#ApplicationLabel: ZxingBarcodeScanner
#VersionCode: 1
#VersionName:
'SupportedOrientations possible values: unspecified, landscape or portrait.
#SupportedOrientations: portrait
#CanInstallToExternalStorage: False
#End Region
#Region Activity Attributes
#FullScreen: False
#IncludeTitle: True
#End Region
Sub Process_Globals
'These global variables will be declared once when the application starts.
'These variables can be accessed from all modules.
End Sub
Sub Globals
'These global variables will be redeclared each time the activity is created.
'These variables can only be accessed from this module.
Private zx1 As ZxingBarcodeScanner
Private b1 As Button
Private b2 As Button
Private b3 As Button
End Sub
Sub Activity_Create(FirstTime As Boolean)
'Do not forget to load the layout file created with the visual designer. For example:
Activity.LoadLayout("main")
zx1.LaserColor = Colors.Yellow
zx1.MaskColor = Colors.ARGB(150, 0, 0, 200)
zx1.BorderColor = Colors.Magenta
zx1.BorderStrokeWidth = 5
zx1.BorderLineLength = 40
zx1.Visible = False
End Sub
Sub Activity_Resume
End Sub
Sub Activity_Pause (UserClosed As Boolean)
zx1.Visible = False
zx1.stopScanner
End Sub
Sub b1_Click
zx1.toggleFlash
End Sub
Sub b2_Click
zx1.Visible = True
zx1.startScanner
End Sub
Sub b3_Click
zx1.Visible = False
zx1.stopScanner
End Sub
Sub zx1_scan_result (scantext As String, scanformat As String)
Log ("B4A scan text = " & scantext)
Log ("B4A scan format = " & scanformat)
End SubThe library:
ZxingBarcodeScanner
Author: Github: Dushyanth Maguluru, Wrapped by: Johan Schoeman
Version: 1
ZxingBarcodeScanner
Events:
- scan_result (scantext As String, scanformat As String)
- ba As BA
- BringToFront
- DesignerCreateView (base As PanelWrapper, lw As LabelWrapper, props As Map)
- Initialize (EventName As String)
- Invalidate
- Invalidate2 (arg0 As Rect)
- Invalidate3 (arg0 As Int, arg1 As Int, arg2 As Int, arg3 As Int)
- IsInitialized As Boolean
- RemoveView
- RequestFocus As Boolean
- SendToBack
- SetBackgroundImage (arg0 As Bitmap)
- SetColorAnimated (arg0 As Int, arg1 As Int, arg2 As Int)
- SetLayout (arg0 As Int, arg1 As Int, arg2 As Int, arg3 As Int)
- SetLayoutAnimated (arg0 As Int, arg1 As Int, arg2 As Int, arg3 As Int, arg4 As Int)
- SetVisibleAnimated (arg0 As Int, arg1 As Boolean)
- handleResult (rawResult As Result)
- startScanner
- stopScanner
- toggleFlash
- android.permission.CAMERA
- android.permission.FLASHLIGHT
- Background As Drawable
- BorderColor As Int [write only]
- BorderLineLength As Int [write only]
- BorderStrokeWidth As Int [write only]
- Color As Int [write only]
- Enabled As Boolean
- Height As Int
- LaserColor As Int [write only]
- Left As Int
- MaskColor As Int [write only]
- Tag As Object
- Top As Int
- Visible As Boolean
- Width As Int
Attachments
Last edited:
