Delauney

[ceaser]

Hi

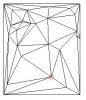
Does anybody know about a compact routine for the delauney theorem. It is where one has a number of Y, X and Z coordinates and these get all connected up by triangles. But the triangles are not allowed to cross each other.

We use this to generate contours, calc volumes, etc.

I have one for the PC, but it is too heavy for a Mobile.

Thanks
Michael

 

[agraham]

I have one for the PC, but it is too heavy for a Mobile.l

This looks interesting , I hadn't realised the significance/importance of an algorithm like this in so many areas of computer graphics and design. In what way is what you have too "heavy" for a device? Simple/compact usually means unoptimised and hence slow - and present devices are hardly computational powerhouses!

I think your interest is surveying is it not? Do you need 3D Delauney or is 2D good enough? How many points would you need to deal with on the device? In what units are the points expressed and in what format would the results be usefull?

 

[ceaser]

Hi Agraham

Yes you right, I am a Land Surveyor & Civil Engineer and programming is more of a hobby for me, although I have 2 commercial programs on the market.

Coming back to the delauney theorem, we call it a Tin Model. Once you have done a tachy survey in the field, digitized an existing drawing, scanned a mine dump, etc. one sits with a file consisting of Y, X and Z coordinates. Now before one can do anything with these points, we need to create a Tin Model (Triangles) of these points. No side of a Triangle is allowed to cross the side of another triangle. And the ideal triangle is where the 3 internal angles are all 60 degrees. Once you have a Tin, one can generate 3D views, solid models, calculate volumes, generate cross sections, longitudinal sections, etc. the list is endless.

You ask how many points? Well this can range from a couple of hundreds to a couple of hundred thousands. And yes the model must be 3D.

If you want I can send you the routine that I have for VB6.

Regards
Michael

 

[agraham]

You ask how many points? Well this can range from a couple of hundreds to a couple of hundred thousands. And yes the model must be 3D.

I meant how many points would be practical, and useful, for a device application.

If you want I can send you the routine that I have for VB6.

Please, I'd like to see it. Ones I have looked at on the Web vary from the fairly simple but long running to the obscurely fiendish accompanied by dense mathematical terms with which I am familiar not!

Why not post it here, if it is not proprietary. Other maths oriented people, like Klaus, might like a look.

 

[agraham]

Are you sure it is a 3D Delauney that you need and not a 2D one that just carries the Z values through? I found this site on terrain modelling Triangulate: Pan Pacific Computer Conference, Beijing, China which has a selection of 2D implementations in various languages. I've implemented the one in C# by Christian Stelzl as a Basic4ppc library. It takes about 23 seconds to calculate 1000 points on my HTC Diamond and a further 35 to plot the resulting triangles rather inefficiently using Form.Line.

 

[taximania]

Possibly OT

How does one plot a 3D such as this one ?

I've downloaded programs that show such images,
but never managed to code similiar myself.

I suspect the 'viewing angle' is the hardest part to achieve.
The rest I know is possible :signOops: just not by me

TIA

 

[agraham]

How does one plot a 3D such as this one ?

Look here 3D projection Ignore the maths and look at the diagram at the end and you can see what is happening.

 

[taximania]

:sign0137:

I'll study this further tomorrow, been busy tonight.

Edit:
BTW: cheers Agraham, it's a start I'd not found on the net.

 

[ceaser]

Hi Agraham

I am flying down to Cape Town on the 8th December, then I will forward you my routine for the delauney triangles. I do not have it here with me at the moment.

You are right about the Z (elevation) value. That value is already there from the height of the tachy point.

I get the impression that your DLL is much more compact than the one that I have for the PC. It's faster!

How would you go about swapping triangles on the screen by tapping on a common side of 2 triangles? Or adding in breaklines?

Regards
Michael

 

[agraham]

It's faster!

I've implemented another variant from that site by Salvatore Previti that is even more optimised and is about three times quicker for 10,000 points on the desktop, 2.3-ish v 6.4i-sh seconds. I haven't tried it on a device. I presume the speed ratio would improve further with more points.

How would you go about swapping triangles on the screen by tapping on a common side of 2 triangles?

How can you "swap" triangles. I thought the measured points determined where the triangles were. Do you mean changing the common edge. If we have two triangles with vertices ABCD clockwise and common edge AC do you mean making the common edge BD? Identifying the two triangles by working back from the screen co-ordinates would be the problem, identifying the common vertices and swapping them would be relatively trivial.

Or adding in breaklines?

What's a breakline and what do you do to the triangles to add it in?

EDIT :- I think I understand breaklines. I found a video demonstrating something called SiteTopo I think and he was adding breaklines manually which seemed to be what you meant by "swapping" triangles. I guess that if you had a list points on a breakline you could search the triangle list and check they were all on common edges - the exact details of such an algorithm elude me at the moment

 

[ceaser]

Hi Agraham

You are right. If you have 2 triangles joining each other say ABC & CDA with AC being the common side, then by tapping on the screen on line AC, the program must make DB the common side. Normally what I do once I have created a Tin model, is to let the program generate contours from the Tin Model. From the contours one can usually pick up that 2 triangles are not drawn in correctly. By swapping these 2 triangles one gets better looking contours which are more representative of what is in the field.

A breakline is a line that you define, so the triangles will not cross this line. Triangles will be generated on either side of this line. I use a breakline to define all manmade features like kerbs, edge of roads, etc.

Thanks
Michael

 

[agraham]

Have a play with this. The dll is different to the previous one so discard the earlier dll and demo. Click on each end of a common edge to swap it. Click on opposing vertices of adjacent triangles to do the same. The opposing swap takes a noticable time on a device as opposed to the common edge swap as the search takes a lot longer. The swaps could be speeded up by moving them into the dll.

I assume that given a set of points that make up a breakline then once the initial triangulation is done you could work along the points of the breakline checking whether each pair of points is on a common edge and if not then swap the edge using the opposing vertices swap algorithm.

 

[klaus]

Hi Andrew,

You did a pretty good job !

I had also googled on the subject but hadn't found the site you found but some others with C source codes, but I am not used to C.

I transposed from the site you mentioned the VB source to B4PPC.
It works well, but unfortunately it is much slower than yours.
I didn't post it for that reason.

I 'played' with your last version with the swapping, I noticed that there should be anouther check for possible swaps.
If you look on the two attached images. The red line should not be generated, in this case the green line is the only possibiliy, because another point is inside the new triangle.

Do do these 'plays' I added to your program a routine to save and load a points set to be able to reproduce the same scheme.
I added the modified program and the points file for the example.

Best regards.

 

[agraham]

I noticed that there should be anouther check for possible swaps

I knew about that but couldn't come up with a quick algorithm for detecting whether another point was in the new triangle. Then I had a flash of inspiration and realised that for a permitted swap the area of the triangles was constant but the area increased for an invalid one!

I've implemented a swap check based on triangle areas and moved the long running "FindTriangle..." routines into the library for speed. It can quite happily cope with at least 200 points on a device now with little user perceived lag apart from the inital triangulation and drawing of triangles.

 

[klaus]

I didn't have a look yet on your new version.

But I was thinking of another algorythm.
If we look at the 2 points not belonging to the new swap line:
- For a 'legal' swap, these 2 points are one on each side of the swap line.
- For an 'illegal' swap they are both on the same side.

I don't know which one needs more calculation time.

Best regards.

 

[agraham]

I- For a 'legal' swap, these 2 points are one on each side of the swap line.- For an 'illegal' swap they are both on the same side.

I couldn't think of a neat algorithm for that - not to say that there isn't one!

 

[klaus]

In the program I transposed from VB, there is a routine to determine on what side of a line a point is.

[FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]
[SIZE=2][FONT=Courier New][COLOR=#0000ff]Private[/COLOR][/FONT][/SIZE][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]Sub [/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][FONT=Courier New][SIZE=2]WhichSide(xp, yp, x1, y1, x2, y2)[/SIZE][/FONT]
[/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#008000][FONT=Courier New][SIZE=2][COLOR=#008000][FONT=Courier New][SIZE=2][COLOR=#008000]'Determines which side of a line the point (xp,yp) lies.[/COLOR][/SIZE][/FONT]
[SIZE=2][FONT=Courier New][COLOR=#008000]'The line goes from (x1,y1) to (x2,y2)[/COLOR][/FONT][/SIZE]
[SIZE=2][FONT=Courier New][COLOR=#008000]'Returns -1 for a point to the left[/COLOR][/FONT][/SIZE]
[SIZE=2][FONT=Courier New][COLOR=#008000]' 0 for a point on the line[/COLOR][/FONT][/SIZE]
[SIZE=2][FONT=Courier New][COLOR=#008000]' +1 for a point to the right[/COLOR][/FONT][/SIZE]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff] Dim[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][FONT=Courier New][SIZE=2] equation[/SIZE][/FONT]
[SIZE=2][FONT=Courier New] equation = ((yp - y1) * (x2 - x1)) - ((y2 - y1) * (xp - x1))[/FONT][/SIZE]
[/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff] If[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][FONT=Courier New][SIZE=2] equation > [/SIZE][/FONT][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080]0[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]Then[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]   Return[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][FONT=Courier New][SIZE=2] -[/SIZE][/FONT][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080]1[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff] Else[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]If[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][FONT=Courier New][SIZE=2] equation = [/SIZE][/FONT][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080]0[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]Then[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]   Return[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080]0[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff] Else[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]   Return[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080][FONT=Courier New][SIZE=2][COLOR=#800080]1[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff] End[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]If[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff][FONT=Courier New][SIZE=2][COLOR=#0000ff]End Sub[/COLOR][/SIZE][/FONT]
[/COLOR][/SIZE][/FONT][/COLOR][/SIZE][/FONT]

Attached the program.

Best regards.

 

[ceaser]

Hi Guys

Wow!:sign0188: You guys are clever!

I am busy with your routine to generate contours based on the Tin Model and later on calculate a volume. Once it is finished, is it possible to move it to the DLL as well please? My knowledge of DLL's is very limited.

Regards
Michael

 

[agraham]

Once it is finished, is it possible to move it to the DLL as well please?

Of course. Just post it (with a test app or demo to cross check the resulting library with) and I will translate and implement it for you.

 

[klaus]

Hi Andrew,

The algorithm, with checking the points on 1 or both sides of the new line works well.

I attached my small test program. You can draw points on the screen, then click on the Swap RadioButton, select a line (not the points) and click on the Swap Button to make the change.

Best regards.