I´m looking at measuring some small routes using GPS, the longest one is like 650 meters, this routes can have several corners. The idea is to have the GPS on and walk the path, click a button on each corner and calc the distances beetween those points. This is already working.
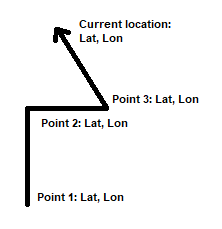
Has anyone drawn GPS data on a canvas? Is there a library or some example code to draw the route scaled to use all the canvas.
Concept:
Thanks
Has anyone drawn GPS data on a canvas? Is there a library or some example code to draw the route scaled to use all the canvas.
Concept:
Thanks