A connected graph is a series of nodes connected with edges.
The edges have a weight (in this example I use 1 for all edges - but any weight will do)
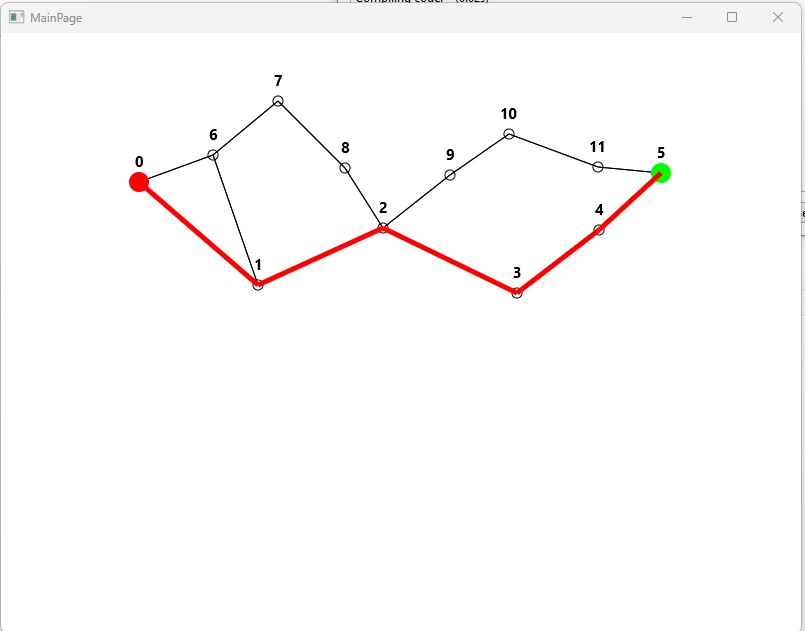
Dijkstra, a Dutch computer scientist thought this up in 20 minutes while out for a cup of coffee.
It was a mental exercise, he says.
It is best understood in reverse.
Consider the nodes with edges going into the target.
"Assume" we know the shortest path to each of those nodes.
Then we can add the corresponding edge weights and take the minimum of those sums.
That would be the shortest path to the target. The node corresponding to the minimum would be on the path.
If we don't know the shortest path to a given node, consider that node the target and repeat the process!
The actual algorithm goes forward by computing the shortest path to all nodes starting with the source.
This algorithm is famous and has been implemented in many computer languages. This is my contribution to B4X.
I have attached the source code with some extras to create various test graphs in B4J.
In the B4A version these extras are not used.
It is fast for small graphs, but time varies rougly as n squared where n is the number of nodes.
For the graph above, it took 35 MICROseconds to complete (I ran it 1000 times to get a total of 35 miliseconds)
On the Android device, it ran about 8x slower.
I searched the B4X Forum, but I couldn't find a source code. It may be as part of Library, I don't know.
The algorithm has wide application in finding the shortest route through various terrains with obstacles.
The edges have a weight (in this example I use 1 for all edges - but any weight will do)
Dijkstra, a Dutch computer scientist thought this up in 20 minutes while out for a cup of coffee.
It was a mental exercise, he says.
It is best understood in reverse.
Consider the nodes with edges going into the target.
"Assume" we know the shortest path to each of those nodes.
Then we can add the corresponding edge weights and take the minimum of those sums.
That would be the shortest path to the target. The node corresponding to the minimum would be on the path.
If we don't know the shortest path to a given node, consider that node the target and repeat the process!
The actual algorithm goes forward by computing the shortest path to all nodes starting with the source.
This algorithm is famous and has been implemented in many computer languages. This is my contribution to B4X.
I have attached the source code with some extras to create various test graphs in B4J.
In the B4A version these extras are not used.
It is fast for small graphs, but time varies rougly as n squared where n is the number of nodes.
For the graph above, it took 35 MICROseconds to complete (I ran it 1000 times to get a total of 35 miliseconds)
On the Android device, it ran about 8x slower.
I searched the B4X Forum, but I couldn't find a source code. It may be as part of Library, I don't know.
The algorithm has wide application in finding the shortest route through various terrains with obstacles.
B4X:
Private Sub solveDijkstra
sourceNode.distanceFromSource = 0
sourceNode.visited = True
Dim notDone As List: notDone.Initialize
For i = 0 To nodes.Size - 1
notDone.Add(i)
Next
Do While notDone.Size > 0
Dim minx As Int = minIndex(notDone)
Dim currentNode As CNode = nodes.Get(notDone.Get(minx))
Dim ID As Int = currentNode.ID
For Each neighbour As CNeighbour In currentNode.neighbours
Dim tempDistance As Int = currentNode.DistanceFromSource + neighbour.weight
If neighbour.nd.visited = False And tempDistance < neighbour.nd.distanceFromSource Then
neighbour.nd.distanceFromSource = tempDistance
neighbour.nd.previousID = ID
End If
Next
currentNode.visited = True
notDone.RemoveAt(minx)
Loop
End Sub
Private Sub minIndex(notDone As List) As Int
Dim minDist As Int = UNKNOWN
Dim minx As Int
For i = 0 To notDone.Size - 1
Dim nd As CNode = nodes.Get(notDone.Get(i))
If nd.distanceFromSource < minDist Then
minDist = nd.distanceFromSource
minx = i
End If
Next
Return minx
End SubAttachments
Last edited:
