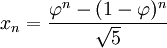Inspired by this thread: https://www.b4x.com/android/forum/threads/a-little-programmers-humor.52576/#post-329226
Create a program that calculates the 300 and 500 numbers in Fibonacci series.
The answers are:
Naive implementation:
Create a program that calculates the 300 and 500 numbers in Fibonacci series.
The answers are:
B4X:
300: 222232244629420445529739893461909967206666939096499764990979600
500: 139423224561697880139724382870407283950070256587697307264108962948325571622863290691557658876222521294125Naive implementation:
B4X:
Sub Fibonacci1(x As Int) As Long
If x = 1 Then Return 1
If x = 2 Then Return 1
Return Fibonacci1(x - 1) + Fibonacci1(x - 2)
End Sub