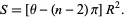/**
* The methods calculates the area on the Earth's spherical enclosed inside a polygon
* which is defined in the list parameter.
* Every list item should be a string of the form "Lat,Long".
* The returned area is in square Km.
*/
public double SphericalArea(List<String> GEOlist)
{
double meanlat = 0;
int n = GEOlist.size() ;
String []str = new String[2] ;
double [][] points = new double[n][2] ; // new array because the content must change
for (int i = 0;i<n;i++)
{
str = GEOlist.get(i).split(",") ;
points[0] = Double.valueOf(str[0])* deg2rad ; // allocation by the index
points[1] = Double.valueOf(str[1])* deg2rad ;
meanlat += points[0];
}
meanlat = meanlat/n ;
return Spherical(points , n, 0, 1, meanlat);
}
private double Spherical(double [][] points , int n, int UindxX, int UindxY, double meanlat)
{
double sum1,sum2,Rs,phis ;
double es = 0.0067394967423 ; // eccentricity
double twoPi = 2 * Math.PI ;
phis = Math.atan(Math.tan(meanlat)/(1+es));
Rs = 6378.137 / Math.pow((1+es*Math.sin(phis)*Math.sin(phis)),0.5); // km
// find angles for point 0
double f1 = Bearing(points[0][0],points[0][1],points[1][0],points[1][1]);
double f2 = Bearing(points[0][0],points[0][1],points[n-1][0],points[n-1][1]);
sum1 = (f1 + twoPi - f2)%twoPi;
sum2 = (f2 + twoPi - f1)%twoPi;
// find angles for point n-1
f1 = Bearing(points[n-1][0],points[n-1][1],points[0][0],points[0][1]);
f2 = Bearing(points[n-1][0],points[n-1][1],points[n-2][0],points[n-2][1]) ;
sum1 += (f1 + twoPi - f2)%twoPi;
sum2 += (f2 + twoPi - f1)%twoPi;
// find angles for the intermediate points
for (int i = 1;i<n-1;i++)
{
f1 = Bearing(points[0],points[1],points[i+1][0],points[i+1][1]);
f2 = Bearing(points[0],points[1],points[i-1][0],points[i-1][1]);
sum1 += (f1 + twoPi - f2)%twoPi;
sum2 += (f2 + twoPi - f1)%twoPi;
}
sum1 = Math.min(sum1,sum2) ; // the minimun is the internal angles sum
return Math.abs((Math.abs(sum1)-(n-2)*Math.PI)) * Rs*Rs ;// in sqr km
}