New video tutorial:
Resumable subs is a new feature added in B4J v5.50 / B4i v4.00 / B4A v7.00. It dramatically simplifies the handling of asynchronous tasks.
(This feature is a variant of stackless coroutines.)
The special feature of resumable subs is that they can be paused, without pausing the executing thread, and later be resumed.
The program doesn't wait for the resumable sub to be continued. Other events will be raised as usual.
Any sub with one or more calls to Sleep or Wait For is a resumable subs. The IDE shows an indicator next to the sub declaration:
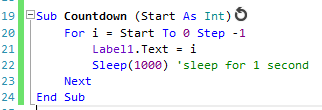
Sleep
Using Sleep is simple:
The sub will be paused for 1000 milliseconds and then be resumed.
You can call Sleep(0) for the shortest pause. This can be used to allow the UI to be refreshed. It is a good alternative to DoEvents (which doesn't exist in B4J and B4i and should be avoided in B4A).
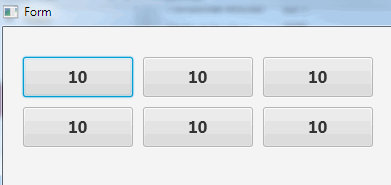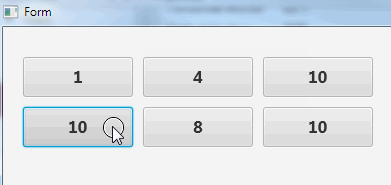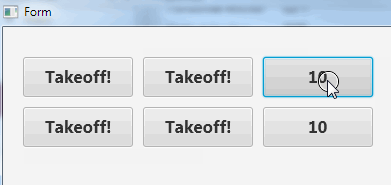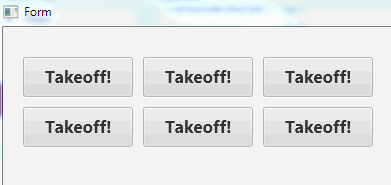
As demonstrated in the following example, each call to a resumable sub creates a different instance which is not affected by other calls:
Wait For
B4X programming language is event driven. Asynchronous tasks run in the background and raise an event when the task completes.
With the new Wait For keyword you can handle the event inside the current sub.
For example, this code will wait for the GoogleMap Ready event:
A bit more complicated example with FTP:
Listing all files in a remote folder and then downloading all the files:
When the Wait For keyword is called, the sub is paused and the internal events dispatcher takes care to resume it when the event is raised. If the event is never raised then the sub will never be resumed. The program will still be completely responsive.
If Wait For is later called with the same event then the new sub instance will replace the previous one.
Lets say that we want to create a sub that downloads an image and sets it to an ImageView:
It will work properly if we call it once (more correctly, if we don't call it again before the previous call completes).
If we call it like this:
Then only the second image will show because the second call to Wait For JobDone will overwrite the previous one.
This brings us to the second variant of Wait For.
To solve this issue Wait For can distinguish between events based on the event sender.
This is done with an optional parameter:
Wait For (<sender>) <event signature>
Example:
With the above code, each resumable sub instance will wait for a different event and will not be affected by other calls.
Code Flow
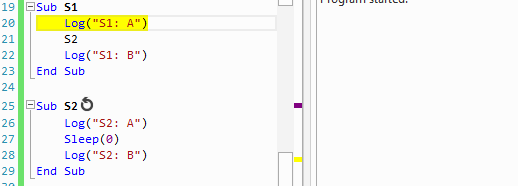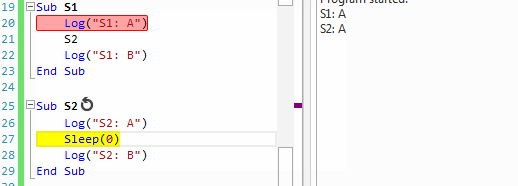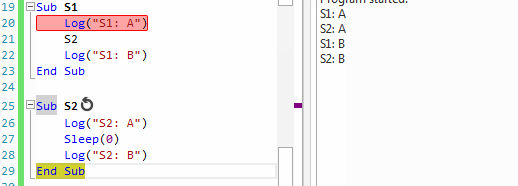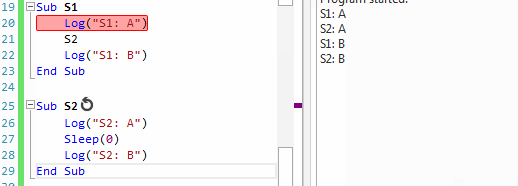
The output is:
S1: A
S2: A
S1: B
S2: B
Whenever Sleep or Wait For are called, the current sub is paused. This is equivalent to calling Return.
Wait for a resumable sub to complete and return values from a resumable sub:
https://www.b4x.com/android/forum/threads/b4x-resumable-subs-that-return-values-resumablesub.82670/
Notes & Tips
- Resumable subs cannot return a value.
- The performance overhead of resumable subs in release mode should be insignificant in most cases. The overhead can be larger in debug mode. (If this becomes an issue then take the slow parts of the code and move them to other subs that are called from the resumable sub.)
- Wait For events handlers precede the regular event handlers.
- Resumable subs do not create additional threads. The code is executed by the main thread, or the handler thread in server solutions.
Resumable subs is a new feature added in B4J v5.50 / B4i v4.00 / B4A v7.00. It dramatically simplifies the handling of asynchronous tasks.
(This feature is a variant of stackless coroutines.)
The special feature of resumable subs is that they can be paused, without pausing the executing thread, and later be resumed.
The program doesn't wait for the resumable sub to be continued. Other events will be raised as usual.
Any sub with one or more calls to Sleep or Wait For is a resumable subs. The IDE shows an indicator next to the sub declaration:

Sleep
Using Sleep is simple:
B4X:
Log(1)
Sleep(1000)
Log(2)You can call Sleep(0) for the shortest pause. This can be used to allow the UI to be refreshed. It is a good alternative to DoEvents (which doesn't exist in B4J and B4i and should be avoided in B4A).
B4X:
Sub VeryBusySub
For i = 1 To 10000000
'do something
If i Mod 1000 = 0 Then Sleep(0) 'allow the UI to refresh every 1000 iterations.
Next
Log("finished!")
End SubAs demonstrated in the following example, each call to a resumable sub creates a different instance which is not affected by other calls:
B4X:
Sub btn_Action
Dim b As Button = Sender
For i = 10 To 0 Step - 1
b.Text = i
Sleep(100)
Next
b.Text = "Takeoff!"
End SubWait For
B4X programming language is event driven. Asynchronous tasks run in the background and raise an event when the task completes.
With the new Wait For keyword you can handle the event inside the current sub.
For example, this code will wait for the GoogleMap Ready event:
B4X:
Sub AppStart (Form1 As Form, Args() As String)
MainForm = Form1
MainForm.RootPane.LoadLayout("1") 'Load the layout file.
gmap.Initialize("gmap")
Pane1.AddNode(gmap.AsPane, 0, 0, Pane1.Width, Pane1.Height)
MainForm.Show
Wait For gmap_Ready '<----------------
gmap.AddMarker(10, 10, "Marker")
End SubA bit more complicated example with FTP:
Listing all files in a remote folder and then downloading all the files:
B4X:
Sub DownloadFolder (ServerFolder As String)
FTP.List(ServerFolder)
Wait For FTP_ListCompleted (ServerPath As String, Success As Boolean, Folders() As FTPEntry, Files() As FTPEntry) '<----
If Success Then
For Each f As FTPEntry In Files
FTP.DownloadFile(ServerPath & f.Name, False, File.DirApp, f.Name)
Wait For FTP_DownloadCompleted (ServerPath2 As String, Success As Boolean) '<-----
Log($"File ${ServerPath2} downloaded. Success = ${Success}"$)
Next
End If
Log("Finish")
End SubWhen the Wait For keyword is called, the sub is paused and the internal events dispatcher takes care to resume it when the event is raised. If the event is never raised then the sub will never be resumed. The program will still be completely responsive.
If Wait For is later called with the same event then the new sub instance will replace the previous one.
Lets say that we want to create a sub that downloads an image and sets it to an ImageView:
B4X:
'Bad example. Don't use.
Sub DownloadImage(Link As String, iv As ImageView)
Dim job As HttpJob
job.Initialize("", Me) 'note that the name parameter is no longer needed.
job.Download(Link)
Wait For JobDone(job As HttpJob)
If job.Success Then
iv.SetImage (job.GetBitmap) 'replace with iv.Bitmap = job.GetBitmap in B4A / B4i
End If
job.Release
End SubIf we call it like this:
B4X:
DownloadImage("https://www.b4x.com/images3/android.png", ImageView1)
DownloadImage("https://www.b4x.com/images3/apple.png", ImageView2)This brings us to the second variant of Wait For.
To solve this issue Wait For can distinguish between events based on the event sender.
This is done with an optional parameter:
Wait For (<sender>) <event signature>
Example:
B4X:
'Good example. Use.
Sub DownloadImage(Link As String, iv As ImageView)
Dim job As HttpJob
job.Initialize("", Me) 'note that the name parameter is no longer needed.
job.Download(Link)
Wait For (job) JobDone(job As HttpJob)
If job.Success Then
iv.SetImage (job.GetBitmap) 'replace with iv.Bitmap = job.GetBitmap in B4A / B4i
End If
job.Release
End SubCode Flow
B4X:
Sub S1
Log("S1: A")
S2
Log("S1: B")
End Sub
Sub S2
Log("S2: A")
Sleep(0)
Log("S2: B")
End SubS1: A
S2: A
S1: B
S2: B
Whenever Sleep or Wait For are called, the current sub is paused. This is equivalent to calling Return.
Wait for a resumable sub to complete and return values from a resumable sub:
https://www.b4x.com/android/forum/threads/b4x-resumable-subs-that-return-values-resumablesub.82670/
Notes & Tips
- The performance overhead of resumable subs in release mode should be insignificant in most cases. The overhead can be larger in debug mode. (If this becomes an issue then take the slow parts of the code and move them to other subs that are called from the resumable sub.)
- Wait For events handlers precede the regular event handlers.
- Resumable subs do not create additional threads. The code is executed by the main thread, or the handler thread in server solutions.
Last edited:
