Share My Creation [B4X] [TOOL][SOURCE] lm Snippets Manager

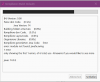
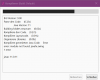
I definitely want to speed up the development of my softwares; I decided to develop a very useful snippets manager.

Although the main purpose is to have all your snippets at your fingertips, saved in a local db, cataloged and easy to find, I have also added the possibility of inserting those that are on b4x.com and also a link to their page.

I am sure that it will also be of use to all the members of our beautiful community.

I'll fill it with my own snippets, as I'm sure you will too, but also the best and most useful ones that are on site.

New version, 3.1.0 (see this post).

NEW Version 3.0.0 - 07/19/2022 - Replaced the import-export part.​

Version 2.3.0 - 03/29/2022 - Added import-export.​

Version 2.2.0 - Added "wildcards" to filter for snippet name. Also added ToolTipTexts. See post #86.

Version 2.1.0 - Added a very useful list of most recent snippets used (window always on top). See post #40.

Ready 2.0.0 version, which implements the feature shown in post #34, code highlighting (which had a hard to solve bug).

Source code - Min. donation: 16 euros.
Obviously you are not allowed to publish/sell the lmSnippetManager source code.

NOTE: to create the stand-alone (exe) version, use:
Download OpenJDK 14.0.1
EDIT: see this post. You have to add javafx folder to that OpenJDK 14.0.1.




Made with love in B4X... of course!!!
 
Last edited:
Click to expand...
angel_

angel_

Well-Known Member
Licensed User
Longtime User
Would it be possible to include wildcards for filtering?

Captura.JPG
 
angel_

angel_

Well-Known Member
Licensed User
Longtime User
If I know it and it works fine but I think it would be useful to be able to introduce wildcards and press show to filter the results
 
LucaMs

LucaMs

Expert
Licensed User
Longtime User
angel_ said:
Would it be possible to include wildcards for filtering?
Click to expand...
"Done".

V. 2.2.0
Done for snippet names (the only useful, I think; for Tags too but this had already been done).
It is not necessary to type asterisks (and you shouldn't), it will search for snippet names containing the entered text.
[Removed the DBSearchView for snippet names, of course]

Also added ToolTipTexts to all cells. (here I filtered on "*image*"):

lmSnippetsManager_220.jpg
 
Last edited:
angel_

angel_

Well-Known Member
Licensed User
Longtime User
LucaMs said:
"Done".

V. 2.2.0
Done for snippet names (the only useful, I think; for Tags too but this had already been done).
It is not necessary to type asterisks (and you shouldn't), it will search for snippet names containing the entered text.
[Removed the DBSearchView for snippet names, of course]

Also added ToolTipTexts to all cells. (here I filtered on "*image*"):

View attachment 111953
Click to expand...
Great feature, thank you!
 
LucaMs

LucaMs

Expert
Licensed User
Longtime User
RauchG

RauchG

Active Member
Licensed User
Longtime User
Hello LucaMS ... I donated € 20 for SnippetManager. Guenter Rauch
 
LucaMs

LucaMs

Expert
Licensed User
Longtime User
RauchG said:
Hello LucaMS ... I donated € 20 for SnippetManager. Guenter Rauch
Click to expand...
Thanks, Guenter.

Unfortunately, I could not share the source with you as Google Drive allows you to do it only with gmail addresses or others that are anyway associated with a gmail.
https://support.google.com/drive/answer/6033939?hl=en

Luckily, the zip file is 497KB, just as big as you can attach here in the forum, so I'm sending it to you in a private conversation.
This way, however, if I update the project in the future...!


Thanks so much again for your generous donation, Guenter.
 
Last edited:
RauchG

RauchG

Active Member
Licensed User
Longtime User
Hi LucaMS ... I have an error message
B4X: 
Waiting for debugger to connect...
Program started.
Fehler in Zeile: 547 (Main)
java.lang.RuntimeException: Method: reorderingProperty not found in: javafx.scene.control.skin.TableHeaderRow
    at anywheresoftware.b4j.object.JavaObject$MethodCache.getMethod(JavaObject.java:363)
    at anywheresoftware.b4j.object.JavaObject.RunMethod(JavaObject.java:120)
    at com.snippetsmanager.lm.main._disablereordering(main.java:519)
    at com.snippetsmanager.lm.main._appstart(main.java:395)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke0(Native Method)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke(NativeMethodAccessorImpl.java:62)
    at java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
    at java.base/java.lang.reflect.Method.invoke(Method.java:566)
    at anywheresoftware.b4a.shell.Shell.runMethod(Shell.java:632)
    at anywheresoftware.b4a.shell.Shell.raiseEventImpl(Shell.java:237)
    at anywheresoftware.b4a.shell.Shell.raiseEvent(Shell.java:167)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke0(Native Method)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke(NativeMethodAccessorImpl.java:62)
    at java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
    at java.base/java.lang.reflect.Method.invoke(Method.java:566)
    at anywheresoftware.b4a.BA.raiseEvent2(BA.java:108)
    at anywheresoftware.b4a.shell.ShellBA.raiseEvent2(ShellBA.java:98)
    at anywheresoftware.b4a.BA.raiseEvent(BA.java:95)
    at com.snippetsmanager.lm.main.start(main.java:38)
    at javafx.graphics/com.sun.javafx.application.LauncherImpl.lambda$launchApplication1$9(LauncherImpl.java:846)
    at javafx.graphics/com.sun.javafx.application.PlatformImpl.lambda$runAndWait$12(PlatformImpl.java:455)
    at javafx.graphics/com.sun.javafx.application.PlatformImpl.lambda$runLater$10(PlatformImpl.java:428)
    at java.base/java.security.AccessController.doPrivileged(Native Method)
    at javafx.graphics/com.sun.javafx.application.PlatformImpl.lambda$runLater$11(PlatformImpl.java:427)
    at javafx.graphics/com.sun.glass.ui.InvokeLaterDispatcher$Future.run(InvokeLaterDispatcher.java:96)
    at javafx.graphics/com.sun.glass.ui.win.WinApplication._runLoop(Native Method)
    at javafx.graphics/com.sun.glass.ui.win.WinApplication.lambda$runLoop$3(WinApplication.java:174)
    at java.base/java.lang.Thread.run(Thread.java:834)
 
LucaMs

LucaMs

Expert
Licensed User
Longtime User
RauchG said:
Hi LucaMS ... I have an error message

B4X: 
Waiting for debugger to connect...
Program started.
Fehler in Zeile: 547 (Main)
java.lang.RuntimeException: Method: reorderingProperty not found in: javafx.scene.control.skin.TableHeaderRow
    at anywheresoftware.b4j.object.JavaObject$MethodCache.getMethod(JavaObject.java:363)
    at anywheresoftware.b4j.object.JavaObject.RunMethod(JavaObject.java:120)
    at com.snippetsmanager.lm.main._disablereordering(main.java:519)
    at com.snippetsmanager.lm.main._appstart(main.java:395)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke0(Native Method)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke(NativeMethodAccessorImpl.java:62)
    at java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
    at java.base/java.lang.reflect.Method.invoke(Method.java:566)
    at anywheresoftware.b4a.shell.Shell.runMethod(Shell.java:632)
    at anywheresoftware.b4a.shell.Shell.raiseEventImpl(Shell.java:237)
    at anywheresoftware.b4a.shell.Shell.raiseEvent(Shell.java:167)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke0(Native Method)
    at java.base/jdk.internal.reflect.NativeMethodAccessorImpl.invoke(NativeMethodAccessorImpl.java:62)
    at java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
    at java.base/java.lang.reflect.Method.invoke(Method.java:566)
    at anywheresoftware.b4a.BA.raiseEvent2(BA.java:108)
    at anywheresoftware.b4a.shell.ShellBA.raiseEvent2(ShellBA.java:98)
    at anywheresoftware.b4a.BA.raiseEvent(BA.java:95)
    at com.snippetsmanager.lm.main.start(main.java:38)
    at javafx.graphics/com.sun.javafx.application.LauncherImpl.lambda$launchApplication1$9(LauncherImpl.java:846)
    at javafx.graphics/com.sun.javafx.application.PlatformImpl.lambda$runAndWait$12(PlatformImpl.java:455)
    at javafx.graphics/com.sun.javafx.application.PlatformImpl.lambda$runLater$10(PlatformImpl.java:428)
    at java.base/java.security.AccessController.doPrivileged(Native Method)
    at javafx.graphics/com.sun.javafx.application.PlatformImpl.lambda$runLater$11(PlatformImpl.java:427)
    at javafx.graphics/com.sun.glass.ui.InvokeLaterDispatcher$Future.run(InvokeLaterDispatcher.java:96)
    at javafx.graphics/com.sun.glass.ui.win.WinApplication._runLoop(Native Method)
    at javafx.graphics/com.sun.glass.ui.win.WinApplication.lambda$runLoop$3(WinApplication.java:174)
    at java.base/java.lang.Thread.run(Thread.java:834)
Click to expand...
https://www.b4x.com/android/forum/threads/b4x-tool-source-lm-snippets-manager.127714/post-811470
and subsequent posts.
 
RauchG

RauchG

Active Member
Licensed User
Longtime User
Hello Luca, I want to create a build standalone package and I get an error message. What can I do?

B4X: 
'#JavaCompilerPath: 14, C:\jdk-14.0.1\bin\javac.exe
'#JavaCompilerPath: 8, C:\Program Files\Java\jdk1.8.0_202\bin\javac.exe
#JavaCompilerPath: 11, C:\Program Files\Java\jdk-11.0.11\bin\javac.exe
'#JavaCompilerPath: 14, D:\B4J\SnippetManager\jdk-14.0.2_windows-x64_bin\jdk-14.0.2\bin\javac.exe
 

Attachments

  • Screenshot 2021-07-01 070518.png
    Screenshot 2021-07-01 070518.png
    32.6 KB · Views: 239
  • Screenshot 2021-07-01 070608.png
    Screenshot 2021-07-01 070608.png
    28.4 KB · Views: 243
You must log in or register to reply here.

Similar Threads

LucaMs
  • Article
B4A Library [B4X] lmB4XTableExt
Replies
13
Views
5K
LucaMs
LucaMs
Erel
  • Article
B4J Tutorial [B4X] Code snippets
Replies
5
Views
5K
Erel
Erel
LucaMs
  • Article
Share My Creation [Source code][B4X][B4XPages] lmPWsManager
2
Replies
24
Views
11K
Colin Evans
Colin Evans
M
  • Article
Other [tool] [B4X] Snippets For B4X - a B4J app
2
Replies
20
Views
6K
mfstuart
M
Erel
  • Locked
  • Article
B4A Class [class][B4X] Google OAuth2
2
Replies
23
Views
33K
Erel
Erel
Top